5 语法制导翻译

约 2954 个字 37 行代码 4 张图片预计阅读时间 10 分钟

什么是语法制导翻译 Syntax-Directed Translation

语法制导翻译使用 CFG 来引导对语言的翻译，是一种 面向文法 的翻译技术。

我们将「编译」工作划分为以下几个阶段：

词法分析
语法分析
语义分析
中间代码生成
- 由于语义分析的结果通常直接被表示成“中间代码”，所以 3&4 通常一起实现，称为「语义翻译」
- 同时，我们可以在进行「语法分析」的同时进行「语义翻译」，这一技术叫做「语法制导翻译」
代码优化
目标代码生成

1 基本思想

如何「表示」语义信息

我们为 CFG 中的 文法符号 设置 语义属性，从而表示语法成分所对应的 语义信息。
以「变量」为例，其语义信息包括：变量类型、值、存储地址 ...

如何「计算」语义信息

语义属性 的「值」是通过与对应文法符号所在的 Production（文法规则）相关联的「语义规则」计算的。
对于给定的输入串 $x$，我们首先构建对应的「语法」分析树，随后通过与对应 Production 相关的 语义规则 计算树中各节点对应的 语义属性值。

1 语法制导定义 SDD

Syntax-Directed Definitions

SDD 是对 CFG 的推广
- 将每个「文法符号」与一个「语义属性集合」相关联
感觉像是一个 Object 带了一堆的属性
- 将每个 Production 与用于计算产生式中各文法符号属性值的一组语义规则相关联
  - 出于计算属性值的考量，语义规则一般被写成表达式的形式
  - 但当语义规则只是用于产生一个 Side Effect 时，可能会被写成过程调用的形式，比如 $print(E.val)$
隐藏了很多具体实现细节，用户不必「显式说明」翻译发生的顺序

1.1 属性

综合属性 Synthesized Attribute

为 Non-Terminal 节点属性时，只能通过本节点/子节点的属性值来定义；
为 Terminal 节点属性时，由「词法分析器」提供值（SSD 中不存在为“终结符”计算属性的语义规则）

以文法 $number_1 \rightarrow number_2 \ digit$ 为例：

其对应的语义规则为 $number_1.val = number_2.val*10 + digit.val$
对应的语法树如下：

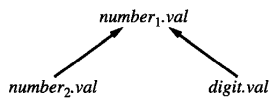
显然，在计算非终结符属性 $number_1.val$ 之前，我们首先需要计算得到两个子节点 $number_2$ 与 $digit$ 的相关属性值

继承属性 Inherited Attribute

为 Non-Terminal 节点属性时，只能通过本节点/父节点/兄弟节点的属性值来定义

=> 与自己的子节点脱钩！

Terminal 没有继承属性（从语法分析中得到的值被认为是“继承属性”）

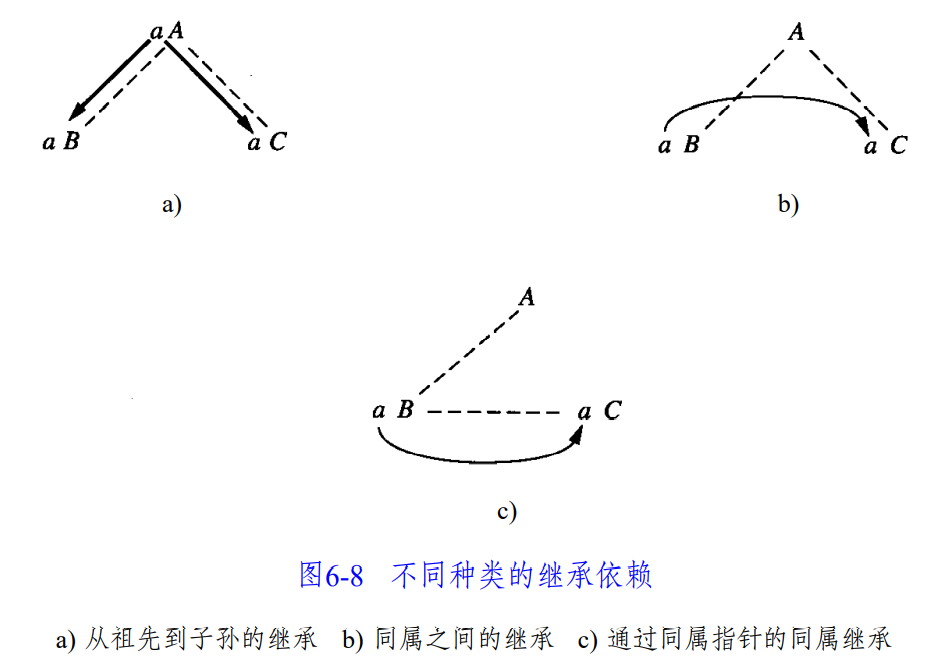
以文法 $D \rightarrow T \ L$ 为例，对应的语义规则为 $L.inh = T.type$ => 值是自左向右传递的（兄弟间传递）

1.2 属性文法 Attribute Grammar

一个没有 Side Effect 的 SDD 有时也被称为“属性文法”
“属性文法”的规则仅通过其他属性值+常量来计算一个属性值

1.3 计算顺序

语义规则建立了 属性之间的依赖关系。在对一个属性进行求值前，我们首先需要计算其所有依赖项的值。

依赖图 Dependency Graph

我们使用有向表示分析树各节点属性之间的依赖关系
- 依赖图节点与语法分析树中的节点属性一一对应
- 出度 = 前置条件，入度 = 存在依赖
因此，我们的任务就变成了找出有向图中的「拓扑顺序」

以字符串 float x, y 为例，其依赖图如下：

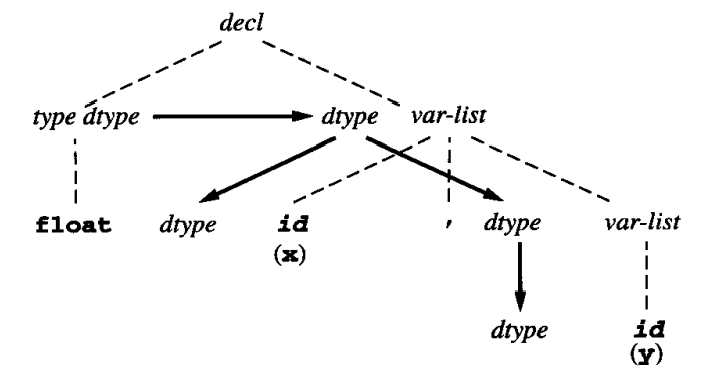
实线表示「依赖传递」关系
虚线只是为了保留语法树的相关结构
我们一般将“继承属性”放在节点左侧，“综合属性”放在节点右侧

对于「只存在综合属性」的 SSD（无环图至少存在一条拓扑顺序），我们可以通过“任意”自底向上的顺序 一次性 完成所有属性的计算
对于同时具有综合属性&继承属性的 SSD（可能出现“环”），我们 可能需要 多次遍历才能完成计算

我们很难确定 SDD 的属性之间是否存在循环依赖关系（有环），存在更有效的方法吗

以下的两个 SDD 子类能够保证每棵语法分析树都存在一个求值顺序（不允许产生环）：

S 属性定义 S-SDD

S-Attributed Definition

只存在「综合属性」，可以通过 任意Bottom-Up 的方法一次性完成计算
每个 S-SDD 都是 L-SDD（只有综合属性）

L 属性定义 L-SDD

L-Attributed Definition

依赖只能「自左向右」，对于 $A \rightarrow X_1X_2X_3...X_n$，$X_n$ 的 继承属性 只能依赖于：
- $A$ 的继承属性（综合属性可能导致循环依赖）
- 其左侧兄弟 $X_1X_2...X_{n-1}$ 的属性
- $X_n$ 本身的属性（但其本身的全部属性不能形成环）
对 综合属性 不做限制

2 语法制导翻译方案 SDT

Syntax-Directed Translation Scheme

是对 SDD 的一种补充，说明了具体的实施方案，显式指明了语义规则的计算顺序。
SDT 是在 Production 右侧嵌入「程序片段」的 CFG，这些片段被称为“语义动作”
按照惯例，“语义动作”需要被书写在一对 {} 内，下面是一个例子： $$ \begin{align} &D \rightarrow T \ {L.inh = T.type}\ L\\ &T \rightarrow int \ {T.type = int}\\ &T \rightarrow real \ {T.type = real}\\ &L \rightarrow {L_1.inh = L.inh}\ L_1,\ id \end{align} $$
“语义动作”在产生式中的位置决定了该动作的 执行时间

2.1 S-SDD → SDT

把语法规则拼接 Production 末尾即可（搞定所有 child 后执行）

如果一个 S-SDD 文法是 LR 的，那么其翻译就可以在 LR 分析过程中实现

=> reduce 时执行语法规则：
1. 当前记录出栈
2. 返回上一状态（上一行的 status）并替换 token
3. 根据新的 token 转换至下一状态
为此，我们需要：
1. 对 LR 分析栈进行扩充 => 添加用于存放 综合属性 的域（可能涉及多个属性）
  - 原本的格式大概是：状态编号 | 当前token
  - 现在搞成：状态编号 | 当前token ｜属性值
2. 将语法规则的抽象定义式改写为可执行的栈操作，下面是一个例子：
  - 栈中依次存放了 Z -> Y -> X（左侧为栈顶）
  - 语法规则为 A.a = f(X.x, Y.y, Z.z)
    
    显然我们需要将 X，Y，Z 出栈进行计算，并将结果 A 入栈保存
  - 改写结果如下：
```
// 1. 结果 A 覆盖 X 的位置
stack[top-2].symb = A;
// 2. 计算 A 的值并保存
stack[top-2].val = f(stack[top-2].val, stack[top-1].val, stack[top].val); 
// 3. 将 X，Y，Z 出栈（X本身已经被覆盖了）
top = top-2; 
```

2.2 L-SDD → SDT

将计算 Non-Terminal 继承属性 的动作插入到该 token 位置之前
将计算左侧符号的 综合属性 的动作放到 Production 末尾

如果一个 L-SSD 文法是 LL 的，那么其翻译就可以在 LL/LR 分析过程中实现

快速判断 LL 文法

具有「相同左部」的 SELECT 集互不相交（FIRST 中有 $\varepsilon$ 时考虑 FOLLOW）

以 $T \rightarrow F\ T'$ 为例，对应了两个语义规则：

$T'.inh = F.val$ => 计算了 T‘ 的 继承属性（从兄弟继承），放到 T' 前
$T.val = T'.syn$ => 计算了左侧 T 的 综合属性，放到末尾

=> 改写结果为 $T \rightarrow F \ \{T'.inh = F.val\} \ T' \ \{T.val = T'.syn \}$

2.2.1 「非递归」分析翻译

扩展语法分析栈

不同的属性具有不同的计算时机：
- 继承属性：在即将出现（前）计算
- 综合属性：在所有子节点完成后计算
在新的栈中包含三种记录类型：
1. action 指向将被执行的动作代码
2. A 非终结符 A 的「继承属性」
3. Asyn 非终结符 A 的「综合属性」
  
  同时存在 A & Asyn 时，Asyn 先入栈（后计算）
为了方便记录，对于代码片段进行编号 $a_1 \ ...\ a_n$
自定向下分析（从 Start Symbol 入栈开始）
- Non-Terminal 入栈时，如果存在需要记录的综合属性，就以 Tsyn + T 的顺序连续进栈
- Non-Terminal 出栈时，根据下一个 token 选择 Production
  - 若 syn 还没计算可以单独保留
  - 若 syn 计算完毕（出栈），需要拷贝到对应的 Action 中
  - 其余 Non-Terminal & Action 逆序进站（FILO）
- 栈顶为 Terminal 时，将匹配的综合属性拷贝给 Action，出栈。
- 栈顶为 Action 时，执行栈操作，出栈。
- 栈顶为 Asyn 时，备份到需要使用该值的 Action 中，出栈。

2.2.2 「递归」预测分析翻译

构建入口函数（给 Start Symbol 对应的函数再套一次皮）

void Desent() {
    D: T.val; // Start Symbol = 'T'，最终结果就是 T 的综合属性 val
    GetNext(token);   // 读取第一个 token
    T.val = T(token); // 调用 Start Symbol 对应的 func，开始处理

    // 如果还有剩余的 token，一定有错误
    if (token != '$') return Error;

    return;
}

我们为每个 Non-Terminal 构造一个函数
- 每个 继承属性 都作为函数的形参
- 综合属性 作为函数的 返回值
- 等式右侧 token 的 每一个属性 都设置一个 局部变量
对于每一个 Production
- 从左到右考虑右侧的 Terminal / Non-Terminal / Action
  - 对于具有综合属性的 Non-Terminal，调用对应的 function（参数是该 Non-Terminal 的所有继承属性），并将返回值赋给存储对应 综合属性 的 局部变量
  - 对于带有综合属性 $x$ 的词法单元 $X$，将其保存在局部变量 $X.x$ 中，随后产生一个匹配 $X$ 的调用，继续输入
  - 对于 Action，直接复制其代码

对于语法规则：

\[ T' \rightarrow \left\{ \begin{align} &* F \ \{T_1'.inh = T'.inh * F.val\}\ T_1' \ \{T'.syn=T_1'.syn\} \\\\ &\varepsilon \ \{T'.syn=T'.inh\} \end{align} \right. \]

我们将其改造为以下函数：

href="#__codelineno-2-1">T'.syn T'(token, T'.inh) { // 为右侧 token 设置局部变量 D: F.val, T1'.inh, T1'.syn; // 根据当前输入 token 决定具体使用那个 Production if (token == '*') then { // 第一条规则 GetNext(token); F.val = F(token); // 调用 func，赋给对应综合属性局部变量 T1'.inh = T'.inh * F.val; GetNext(token); T1'.syn = T1'(token, T1'.inh); T'.syn = T1'.syn; return T'.syn; } else if (token == '$') then { // 第二条规则 T'.syn = T'.inh; return T'.syn; } else { return Error; } }

2.2.3 L-属性的自底向上翻译

给定一个 LL 的 L-SSD 文法，我们可以通过一定修改使之在 LR 上成立：

我们首先对 SDT 进行构造，在每个 Non-Terminal 前设置一个 Action 用于计算其 继承属性，在 Production 设置 Action 用于计算 综合属性
对于 内嵌语义动作，我们引入「标记非终结符」进行替换（Unique），具有一个 Empty Production
- 我们将原 Action 中的需要的、位于该 Action 左侧 token（包括左值）的所有属性作为「非标记终结符」的 继承属性 进行复制
- 按照原 Action 中的方法计算，并将结果作为「非标记终结符」的 综合属性

以下文法由于规则 1&2 中的首个 Action 导致不能直接进行 Bottom-Up 翻译：

\[ \begin{align} &T \rightarrow F \{T'.inh = F.val\} T'\{T.val=T'.syn\}\\\\ &T\ \rightarrow * F\{T_1'.inh = T'.inh * F.val\}T_1'\{T'.syn = T_1'.syn\}\\\\ &T' \rightarrow \varepsilon \{T'.syn = T'.inh\}\\\\ &F \rightarrow digit \{F.val=digit.lexval\} \end{align} \]

我们使用「标记非终结符 Marker Nonterminal」 $M, N$ 对这两个 Action 进行替换，有：

\[ \begin{align} &T \rightarrow F M T'\{T.val=T'.syn\}\\\\ &M \rightarrow \varepsilon \{T'.inh = F.val; M.s=M.i\}\\\\ &T \rightarrow * F N T_1'\{T'.syn = T_1'.syn\}\\\\ &N \rightarrow \varepsilon \{N.i_1=T'.inh;N.i_2=F.val;N.s=N.i_1*N.i_2\}\\\\ &T' \rightarrow \varepsilon \{T'.syn = T'.inh\}\\\\ &F \rightarrow digit \{F.val=digit.lexval\} \end{align} \]

添加的非标记终结符 $M,N$ 都只有一个 Empty Production，用于执行被替换的语义动作
- 虽然 $M,N$ 看似使用了“非法的属性”（$T',F$ 并未在 Production 中出现），但由于采用 LR Parsing，此时这两个数据已经存在栈中
修改完成后，所有的语义动作均位于 Production 的末尾 => 可以直接 Bottom-Up 了
根据后一个 token 进行 reduce -> 弹出栈顶与 Production 右侧吻合的几个 token，压入左式（根据末尾的 Action 计算），并回到前一个 token 所在的状态开始迁移

我们可以将改写 SDT 中的 Action 编写代码：

1.  // T.val = 最右token.syn（栈顶），且顶替 F 进行存储
    T -> FMT'{stack[top-2].val = stack[top].syn; top -= 2;}
    // M 入栈（存储 T'.inh），依赖 F.val 此时正在栈顶
    M -> NULL {stack[top+1].T'inh = stack[top].val; top += 1;}
2.  // T'.syn = 最右token.syn，顶替 * 进行存储
    T' -> *FNT1' {stack[top-3].syn = stack[top].syn; top -= 3;}
    // N 入栈（存储 T1'.inh）
    N -> NULL {stack[top+1].T1'inh = stack[top-2].T'inh * stack[top].val; top += 1;}
3.  // T' 入栈
    T' -> NULL {stack[top+1] = stack[top].T'inh; top += 1;}
4.  // F 替换 digit 存储
    F -> digit {stack[top].val = stacktop.lexval;}

5 语法制导翻译

1 基本思想

1 语法制导定义 SDD

1.1 属性

综合属性 Synthesized Attribute

继承属性 Inherited Attribute

1.2 属性文法 Attribute Grammar

1.3 计算顺序

依赖图 Dependency Graph

S 属性定义 S-SDD

L 属性定义 L-SDD

2 语法制导翻译方案 SDT

2.1 S-SDD → SDT

2.2 L-SDD → SDT

2.2.1 「非递归」分析翻译

2.2.2 「递归」预测分析翻译

2.2.3 L-属性 的自底向上翻译

2.2.3 L-属性的自底向上翻译